Quick-Start Guide¶

The goal is this document is to build the pipeline you see below.

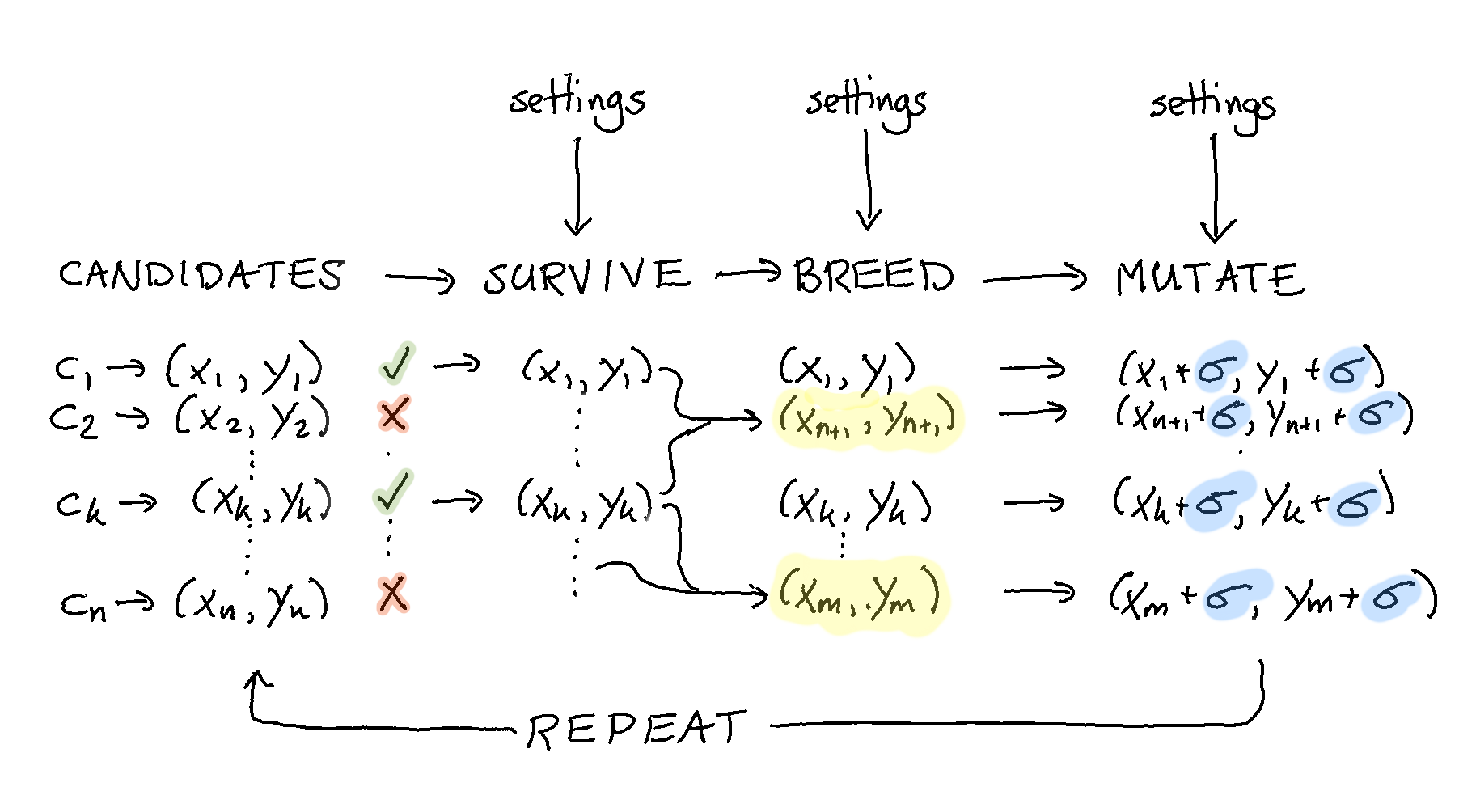
This guide will offer a step by step guide on how to use evol to write custom heuristic solutions to problems. As an example we will try to optimise the following non-linear function:

\(f(x, y) = -(1-x)^2 - (2 - y^2)^2\)

Step 1: Score¶

The first thing we need to do for evol is to describe how “good” a solution to a problem is. To facilitate this we can write a simple function.

def func_to_optimise(xy):
    """
    This is the function we want to optimise (maximize)
    """
    x, y = xy
    return -(1 - x) ** 2 - (2 - y ** 2) ** 2

You’ll notice that this function accepts a “solution” to the problem and it returns a value. In this case the “solution” is a list that contains two elements. Inside the function we unpack it but the function that we have needs to accept one “candidate”-solution and return one score.

Step 2: Sample¶

Another thing we need is something that can create random candidates. We want our algorithm to start searching somewhere and we prefer to start with different candidates instead of a static set. The function below will generate such candidates.

def random_start():
    """
    This function generates a random (x,y) coordinate
    """
    return (r() - 0.5) * 20, (r() - 0.5) * 20

Note that one candidate from this function will create a tuple; one that can be unpacked by the function we’ve defined before.

Step 3: Create¶

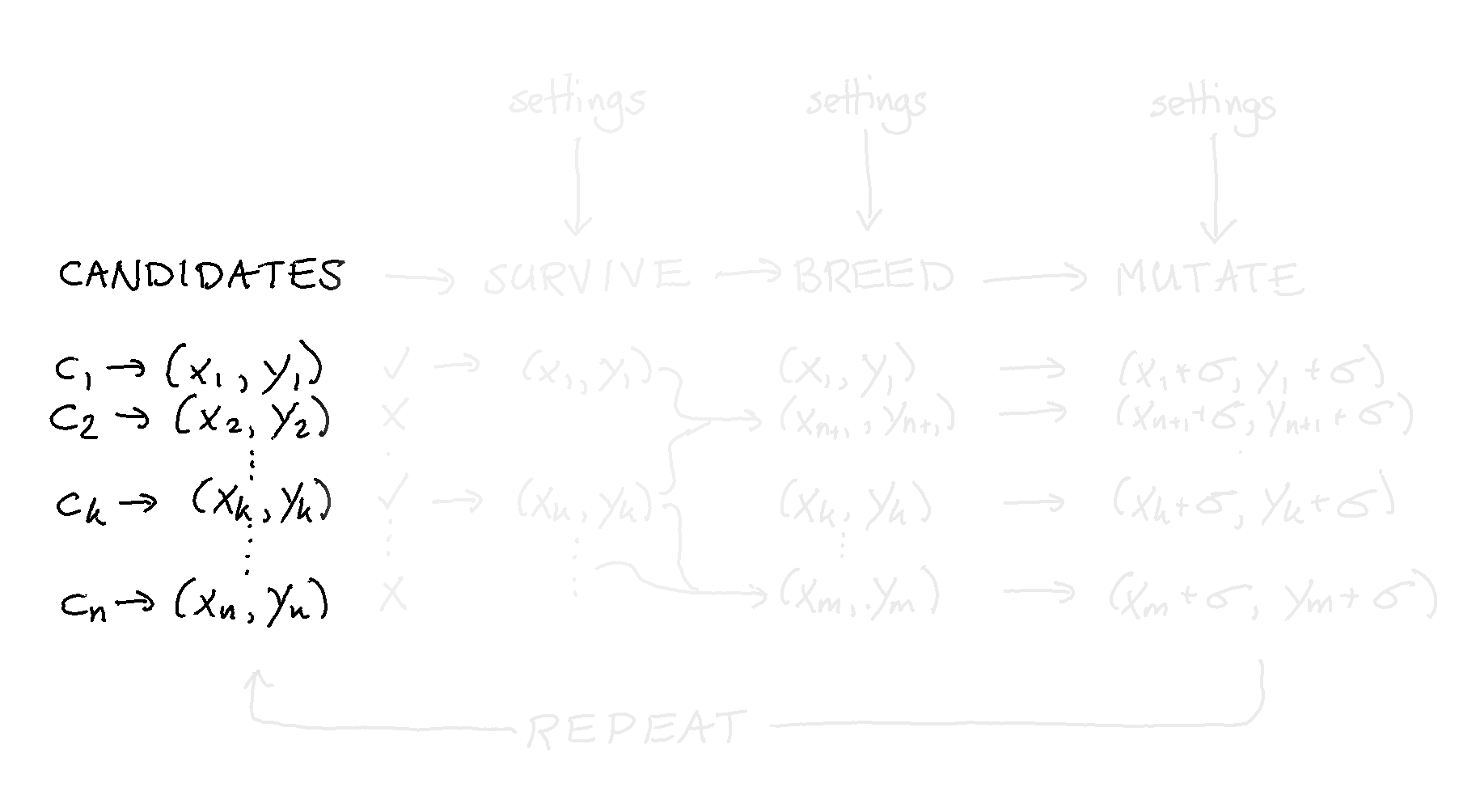
With these two functions we can create a population of candidates. Below we generate a population with 200 random candidates.

pop = Population(chromosomes=[random_start() for _ in range(200)],
                 eval_function=func_to_optimise, maximize=True)

This population object is merely a container for candidates. The next step is to define things that we might want to do with it.

If we were to draw where we currently are, it’d be here:

Step 4: Survive¶

Now that we have a population we might add a bit of code that can remove candidates that are not performing as well. This means that we add a step to our “pipeline”.

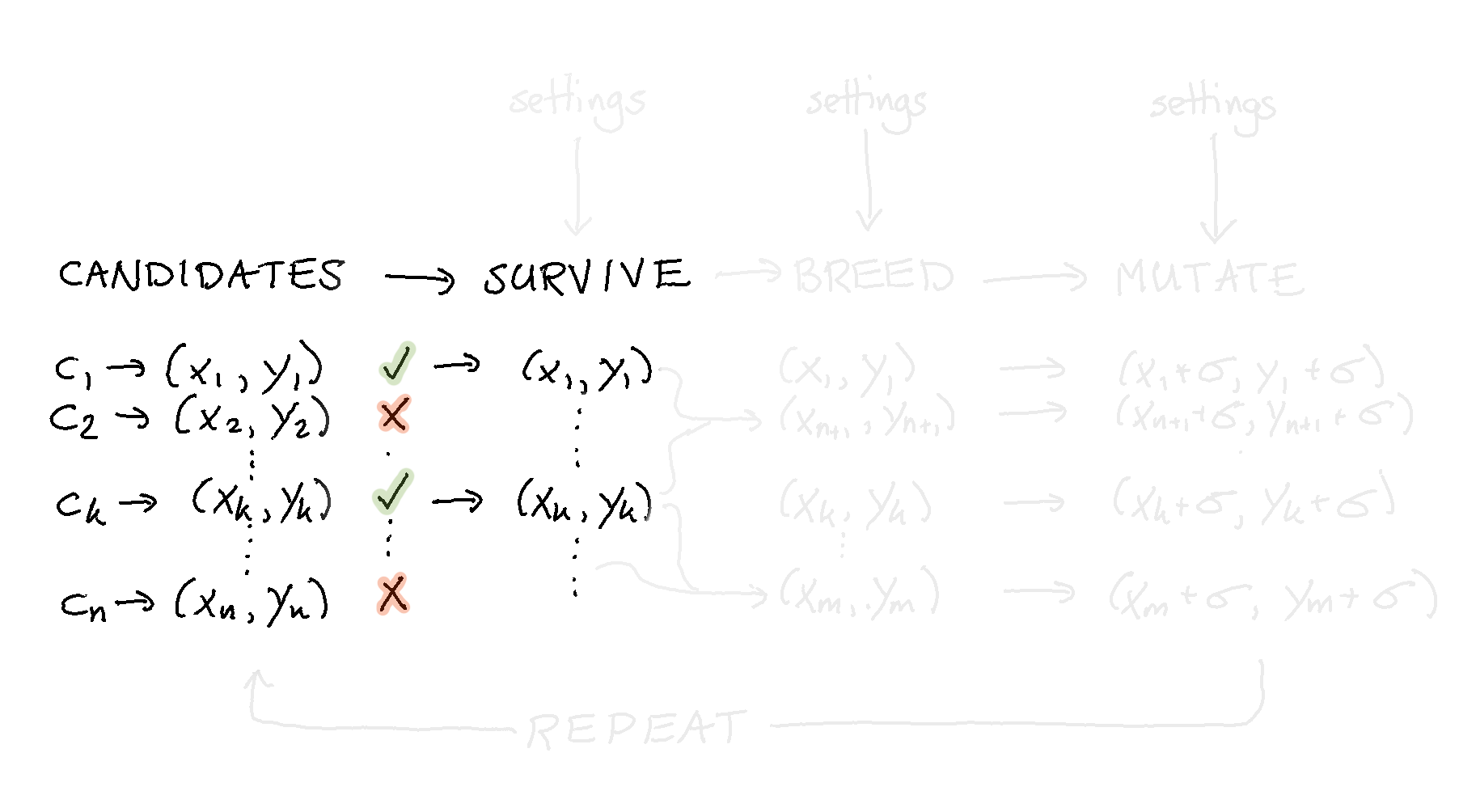
To facilitate this we merely need to call a method on our population object.

# We do a single step here and out comes a new population
pop.survive(fraction=0.5)

Because the population knows what it needs to optimise for it is easy to halve the population size by simply calling this method. This method call will return a new population object that has fewer members. A next step might be to take these remaining candidates and to use them to create new candidates that are similar.

Step 5: Breed¶

In order to evolve the candidates we need to start generating new candites again. This adds another step to our pipeline:

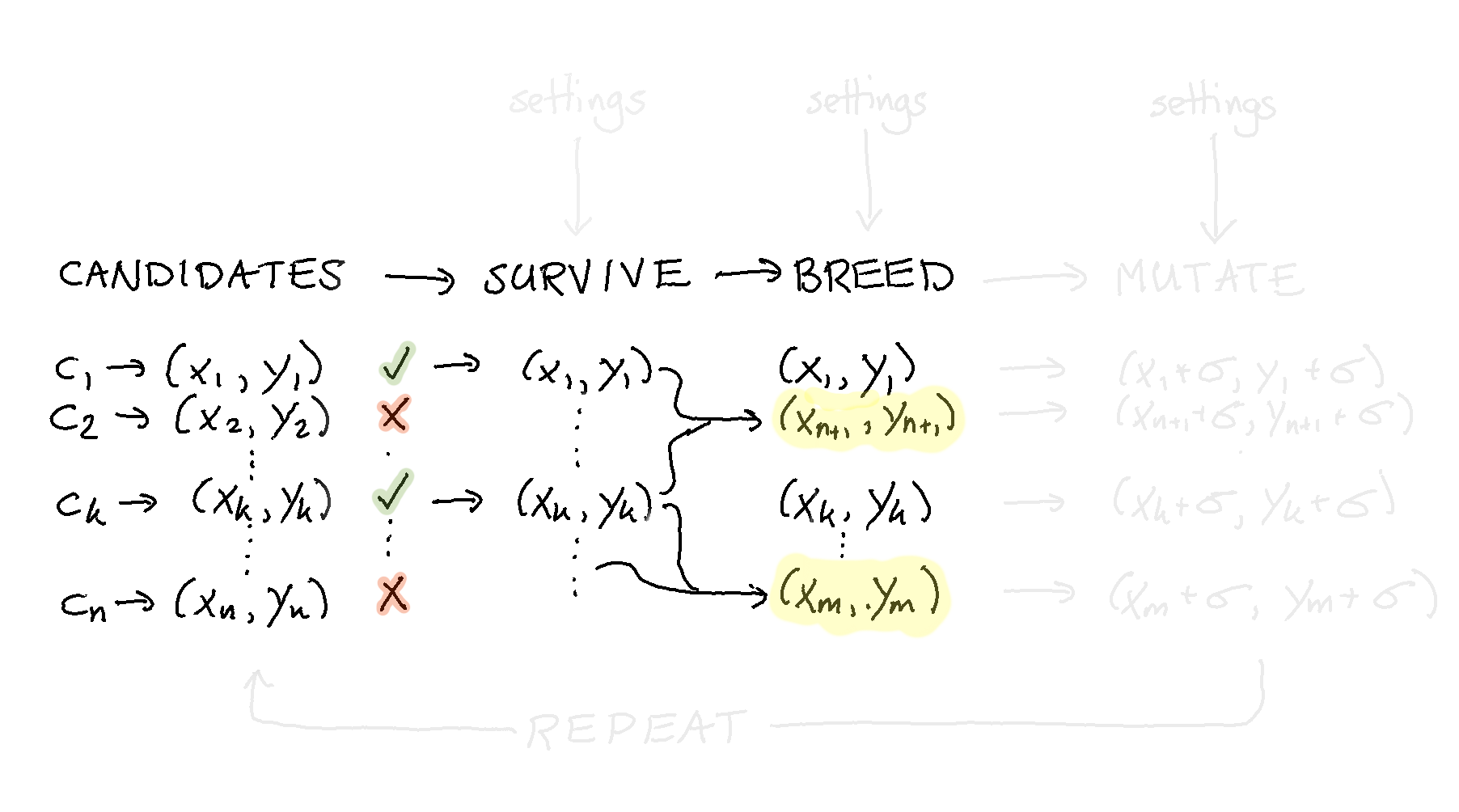
Note that in this view the highlighted candidates are the new ones that have been created. The candidates who were already performing very well are still in the population.

To generate new candidates we need to do two things:

we need to determine what parents will be used to create a new individual
we need to determine how these parent candidates create a new one

Both steps needs to be defined in functions. First, we write a simple function that will select two random parents from the population.

def pick_random_parents(pop):
    """
    This is how we are going to select parents from the population
    """
    mom = random.choice(pop)
    dad = random.choice(pop)
    return mom, dad

Next we need a function that can merge the properties of these two parents such that we create a new candidate.

def make_child(mom, dad):
    """
    This function describes how two candidates combine into a
    new candidate. Note that the output is a tuple, just like
    the output of `random_start`. We leave it to the developer
    to ensure that chromosomes are of the same type.
    """
    child_x = (mom[0] + dad[0]) / 2
    child_y = (mom[1] + dad[1]) / 2
    return child_x, child_y

With these two functions we can expand our initial pipeline and expand it with a breed step.

# We do two steps here and out comes a new population
(pop
 .survive(fraction=0.5)
 .breed(parent_picker=pick_random_parents, combiner=make_child))

Step 6: Mutate¶

Typically when searching for a good candidate we might want to add some entropy in the system. The idea being that a bit of random search might indeed help us explore areas that we might not otherwise consider.

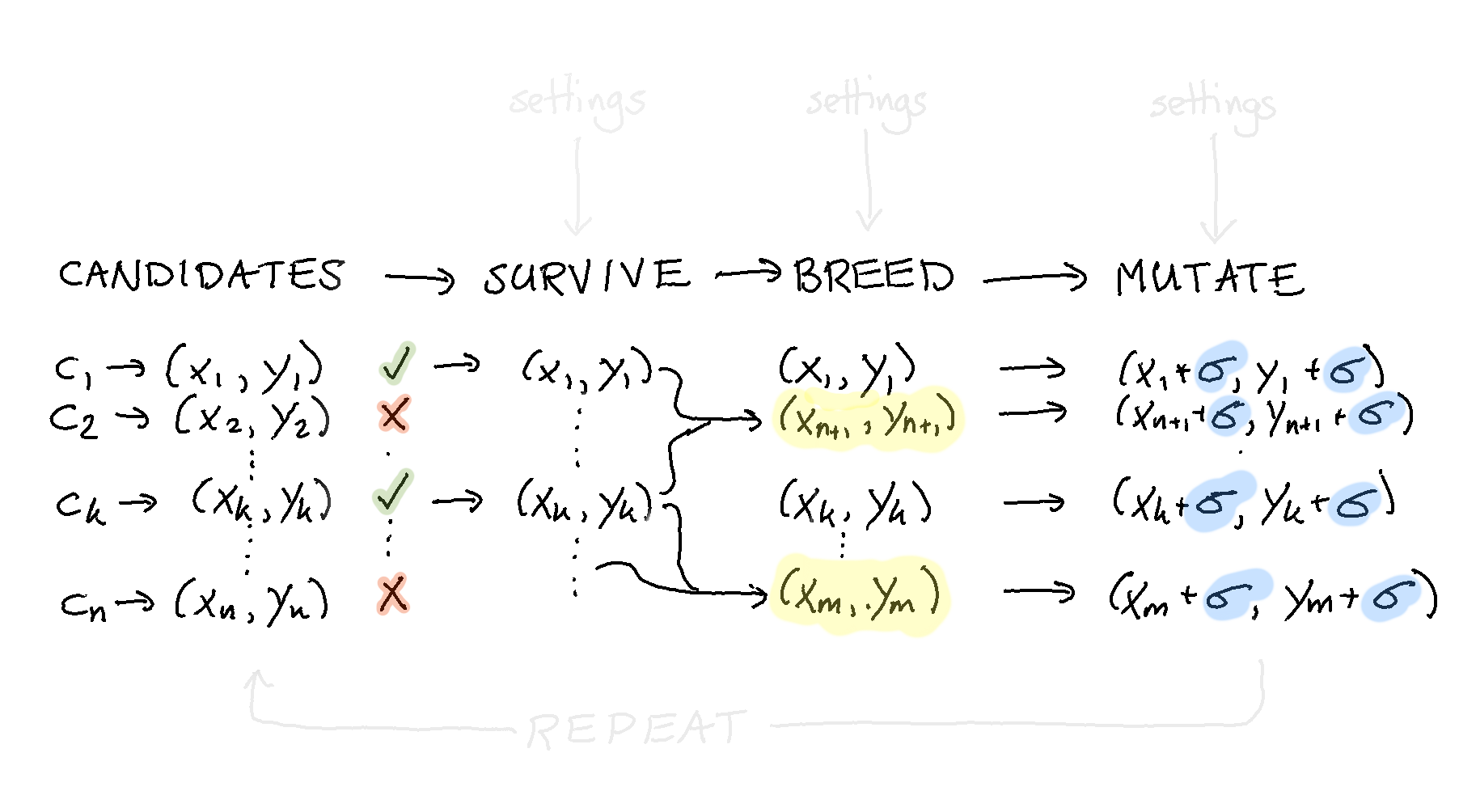
The idea is to add a bit of noise to every single datapoint. This ensures that our population of candidates does not converge too fast towards a single datapoint and that we are able to explore the search space.

To faciliate this in our pipeline we first need to create a function that can take a candidate and apply the noise.

def add_noise(chromosome, sigma):
    """
    This is a function that will add some noise to the chromosome.
    """
    new_x = chromosome[0] + (r() - 0.5) * sigma
    new_y = chromosome[1] + (r() - 0.5) * sigma
    return new_x, new_y

Next we need to add this as a step in our pipeline.

# We do a three steps here and out comes a new population
(pop
 .survive(fraction=0.5)
 .breed(parent_picker=pick_random_parents, combiner=make_child)
 .mutate(mutate_function=add_noise, sigma=1))

Step 7: Repeat¶

We’re getting really close to where we want to be now but we still need to discuss how to repeat our steps.

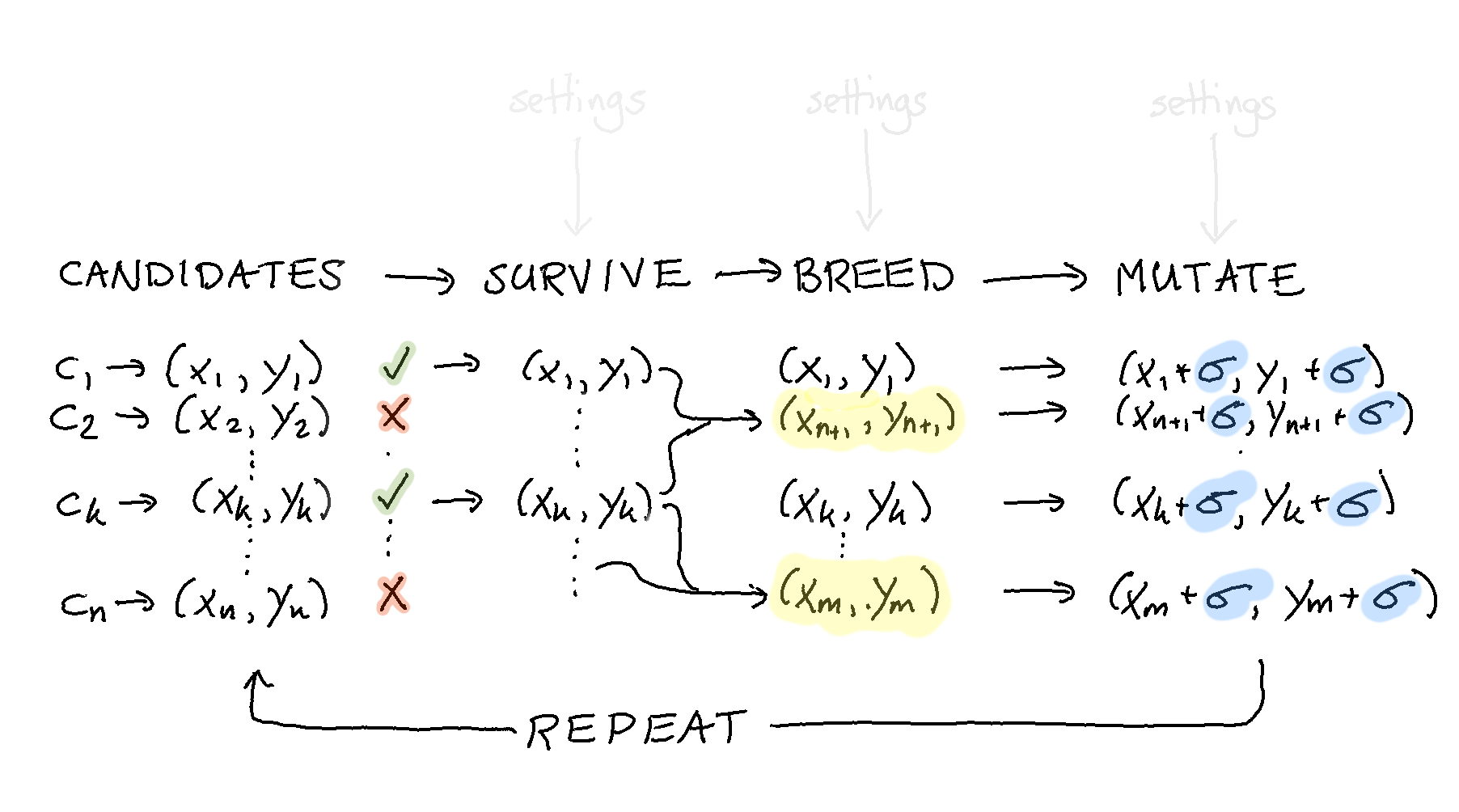
One way of getting there is to literally repeat the code we saw earlier in a for loop.

# This is inelegant but it works.
for i in range(5):
    pop = (pop
           .survive(fraction=0.5)
           .breed(parent_picker=pick_random_parents, combiner=make_child)
           .mutate(mutate_function=add_noise, sigma=1))

This sort of works, but there is a more elegant method.

Step 8: Evolve¶

The problem with the previous method is that we don’t just want to repeat but we also want to supply settings to our evolution steps that might change over time. To facilitate this our api offers the Evolution object.

You can see a Population as a container for candidates and can Evolution as a container for changes to the population. You can use the exact same verbs in the method chain to specify what you’d like to see happen but it allows you much more fledixbility.

The code below demonstrates an example of evolution steps.

# We define a sequence of steps to change these candidates
evo1 = (Evolution()
        .survive(fraction=0.5)
        .breed(parent_picker=pick_random_parents, combiner=make_child)
        .mutate(mutate_function=add_noise, sigma=1))

The code below demonstrates a slightly different set of steps.

# We define another sequence of steps to change these candidates
evo2 = (Evolution()
        .survive(n=1)
        .breed(parent_picker=pick_random_parents, combiner=make_child)
        .mutate(mutate_function=add_noise, sigma=0.2))

Evolutions are kind of flexible, we can combine these two evolutions into a third one.

# We are combining two evolutions into a third one.
# You don't have to but this approach demonstrates
# the flexibility of the library.
evo3 = (Evolution()
        .repeat(evo1, n=50)
        .repeat(evo2, n=10)
        .evaluate())

Now if you’d like to apply this evolution we’ve added a method for that on top of our evolution object.

# In this step we are telling evol to apply the evolutions
# to the population of candidates.
pop = pop.evolve(evo3, n=5)
print(f"the best score found: {max([i.fitness for i in pop])}")

Step 9: Dream¶

These steps together give us an evolution program depicted below.

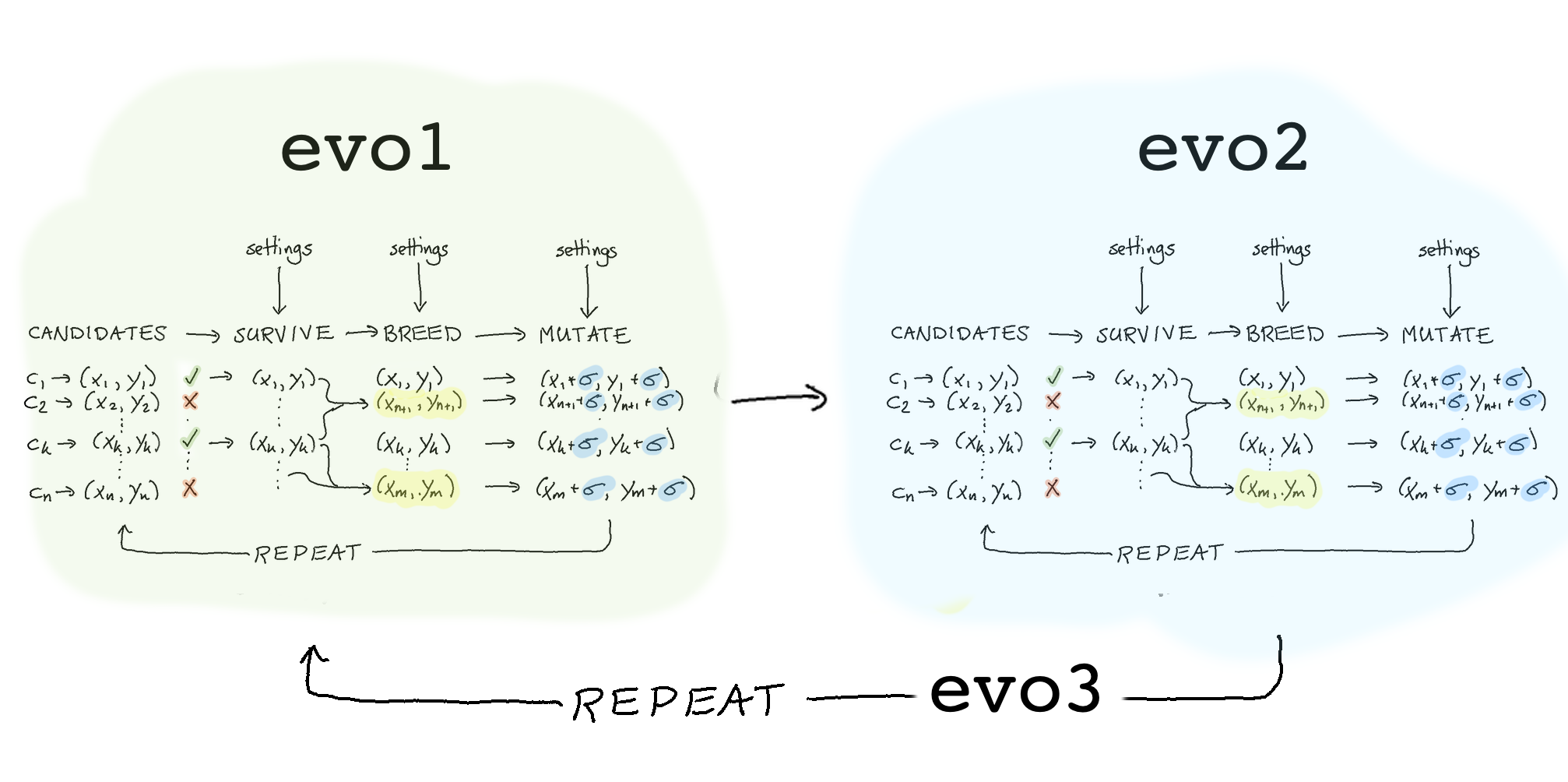
The goal of evol is to make it easy to write heuristic pipelines that can help search towards a solution. Note that you don’t need to write a genetic algorithm here. You could also implement simulated annealing in our library just as easily but we want to help you standardise your code such that testing, monitoring, parallism and checkpoint becomes more joyful.

Evol will help you structure your pipeline by giving a language that tells you what is happening but not how this is being done. For this you will need to write functions yourself because our library has no notion of your specific problem.

We hope this makes writing heuristic software more fun.